From properties to observables
In our previous entry, we have seen how in 1925 the worldview incorporated in physics was forever altered. Gone were any remaining notions of the world as a kind of mechanism, largely independent of human beings trying to make sense of it. Instead of determinism, probability appeared at the core of the new formalism of quantum mechanics.
In classical mechanics, before 1925, physics dealt with objects that had observable properties that could be measured, through observations with various kinds of apparatus. Once observed, if carefully done, those properties would no longer change. Whatever was observable, once observed, was known and remained known. And indeed, for objects on a human scale, and even those on a microscopic scale, these were reasonable conclusions, based on experience. However, this view turned out to be incorrect when investigated at atomic and subatomic scales.
Afterwards, in quantum mechanics, the understanding changed completely. Objects still had characteristics, but they were no longer called properties. Rather, they were given a new name, "observables", something that could be found as an outcome for any act of observation, but most of those outcomes would not be reproducible. There was nothing fixed beforehand that could be observed in its totality. Rather, there was a potential for making observations with different outcomes, each of which were in principle "observable". The only remaining certainty was that the probabilities for specific outcomes remained the same, when repeating an experiment many times, starting from the same initial conditions.
Quick unification of matrix mechanics and wave mechanics
The mathematical equations for determining the probabilities were discovered soon after 1925, but the interpretation of what was going on during a measurement remained completely unclear, as indicated in Fig. 20, reproduced here from entry #010, below.
At first, the only successful equations describing quantum mechanical effects were of two types: Heisenberg's discovery of what would soon be called matrix mechanics, and Schrödinger's wave equation. Soon those were shown to be compatible, presenting two different ways of viewing the same reality. However, both were developed as variations of classical mechanics, and as such were incompatible with special relativity, let alone with general relativity.
The beauty of physics lies in its response to seemingly divergent approaches yielding the same results. Rather than engaging in hostile debates over which method is "truly correct" or settling for a polite compromise where each side sticks to their own view, physicists relentlessly pursue a deeper understanding. They won't rest until they uncover why two fundamentally different models can produce identical outcomes, even if it takes a year or more to figure it out.
Interestingly, this perfectionist approach is similar to that used by computer scientists when they debug a computer program, but in the sense of being exactly the opposite. When professional computer programmers test a new code and then find a small discrepancy in the output, compared to what was expected, they don't just assume that such a small difference doesn't matter. Rather, they realize that this could be a sign of a "bug", an error in a computer program that in some cases could give a slightly different output, but in other cases might give a huge and possibly even disastrously wrong result. For this reason, debugging, finding "bugs" in a computer program, is an essential aspect of software development.
Where computer programmers are alarmed upon finding slight differences, possibly pointing to a bug in their program, theoretical physicists are alarmed when they see no differences at all between two very different approaches. Getting to the bottom of why there is a lack of discrepancies is as important for them as it is for computer scientists to locate a hard-to-find bug. A nagging bug can be a golden opportunity to learn something new about the structure of the program. And a nagging correspondence similarly can be a golden opportunity to attain deeper insight into a theory.
Slow unification of quantum mechanics and special relativity
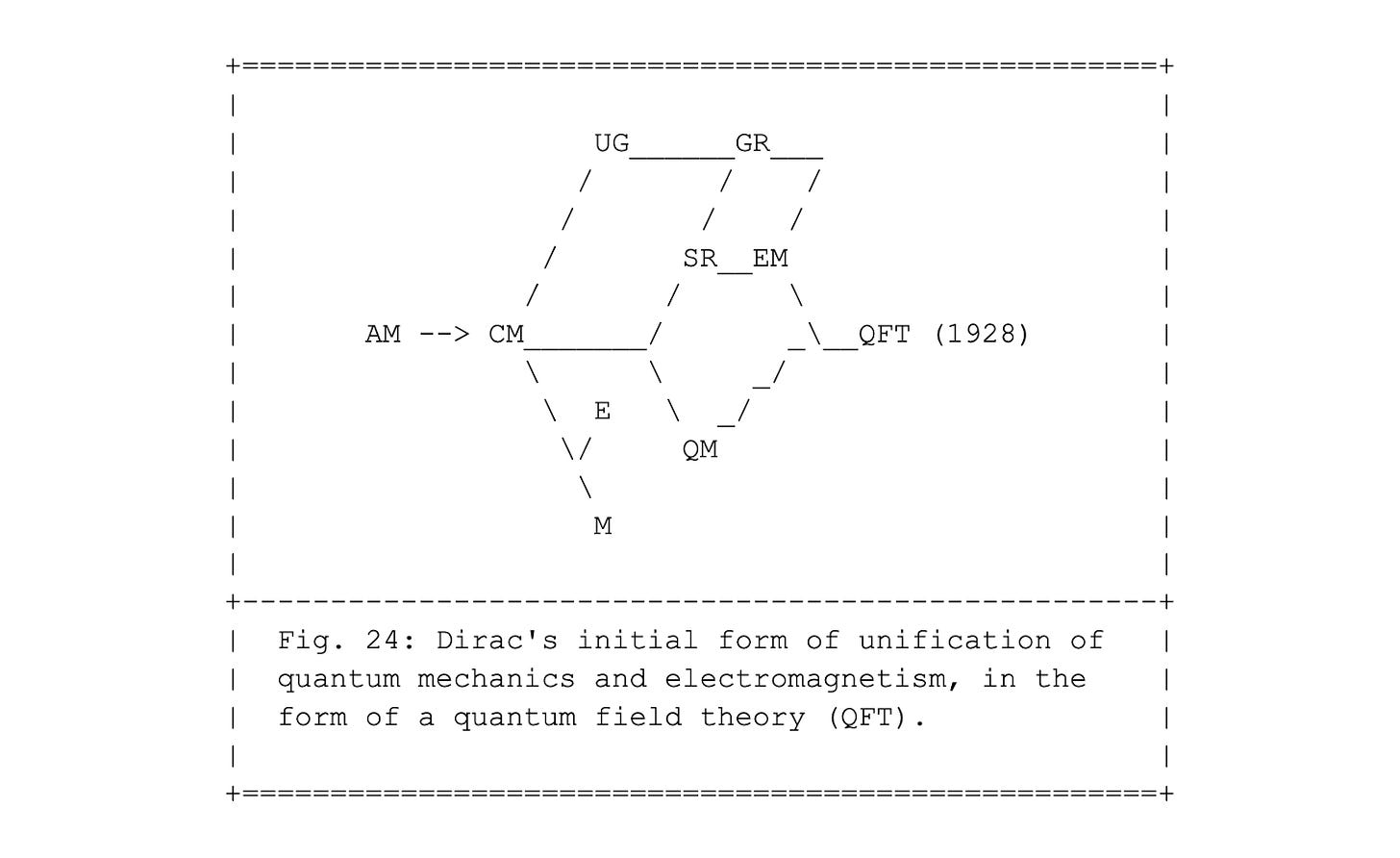
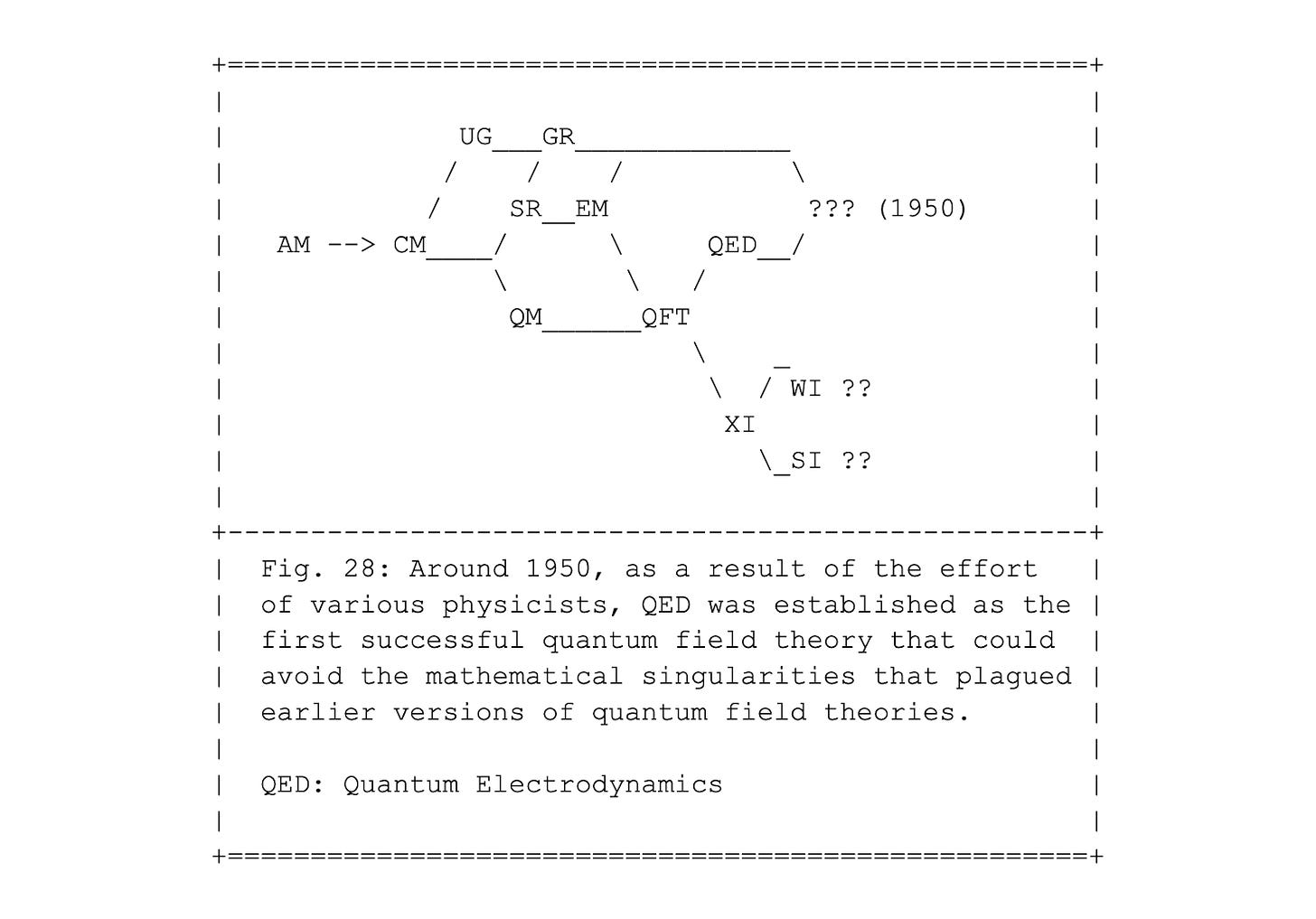
In fig. 20, the "???"indicate an incompatibility gap, separating special relativity (SR) and electromagnetism (EM) in the upper half and the non-relativistic treatments of electricity (E) and magnetism (M) in the lower half. Initially there was rapid progress toward unification across that gap. It would take only three years until at least a partial solution would be found, by Dirac in 1928. He was able to write an equation describing a relativistic generalization of Schrödinger's wave equation. The result was the configuration shown in Fig. 24.
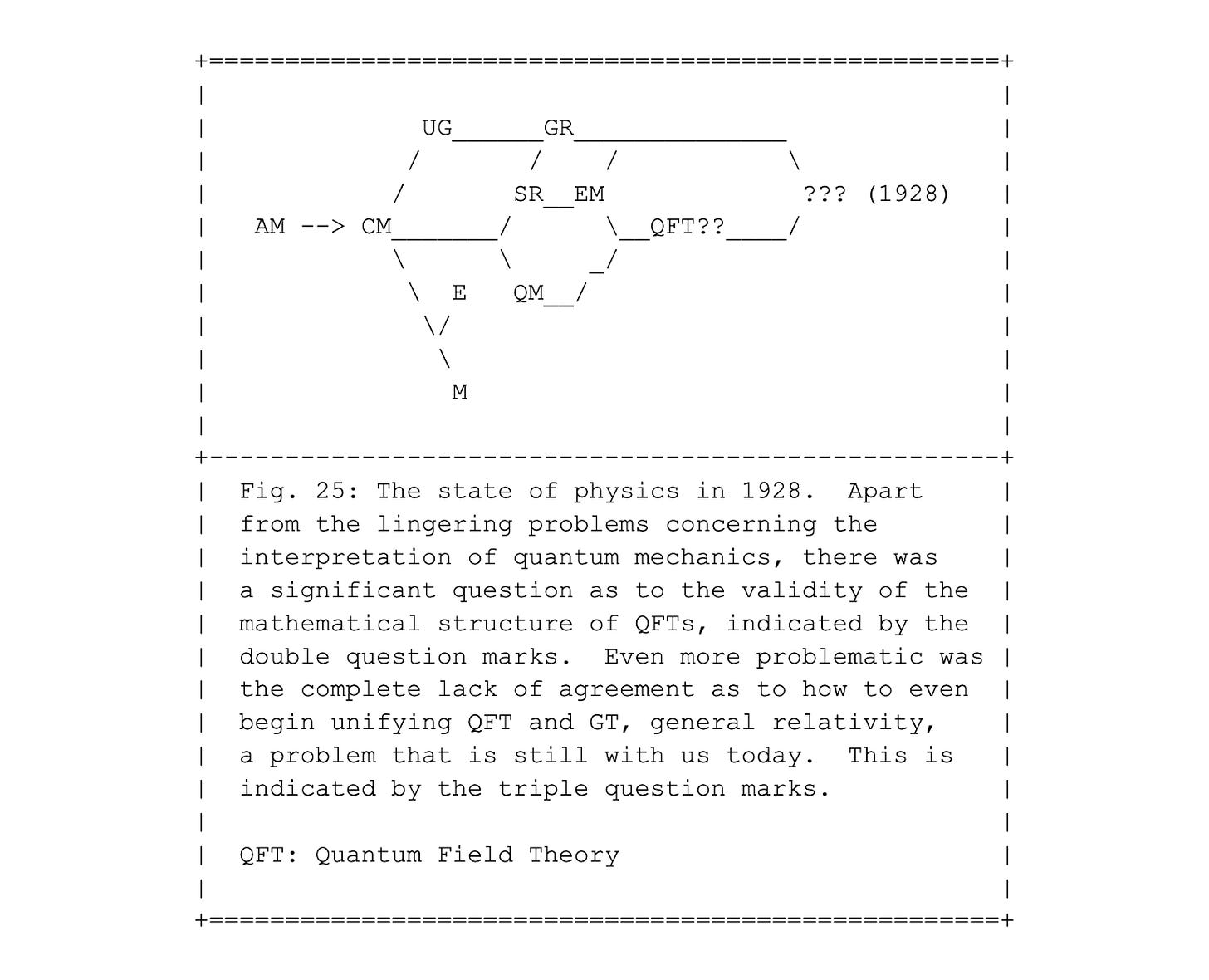
Dirac's equations formed the first example of what is called a Quantum Field Theory (QFT) the name used for theories that unify quantum mechanics (QM) with the relativistic electromagnetic field, which is at the core of electromagnetism (EM). While various predictions were confirmed by experiment, there were still some serious questions about the validity of the mathematical structure of Dirac's equations, and that of subsequent versions of quantum field theories, as indicated in Fig. 25. It would take until 1950 to resolve these difficulties. It was only then that a real unification of quantum mechanics and electromagnetism achieved, under the name of QED, quantum electrodynamics.
New kids on the block: weak and strong interactions
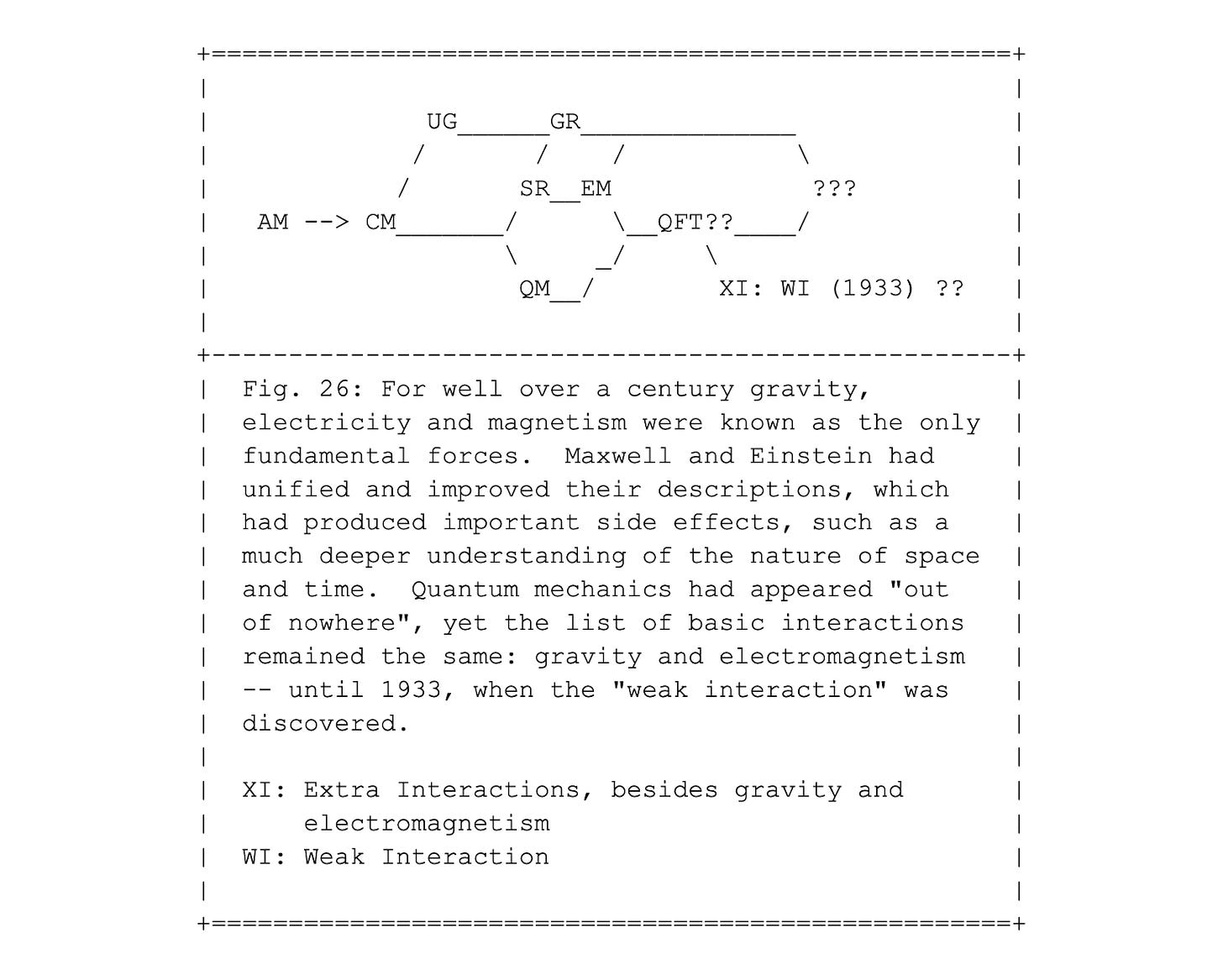
The existence of gravity, by whatever name, has been obvious from time immemorial. Things fall down and don't flow up, unless emerged in some buoyant medium. In entry #008 we saw a brief history of how electricity and magnetism entered the mainstream of physics around 1800, as two additional forces acting at a distance, beyond the force of gravity, depicted in Fig. 4. The forces were seen to be carried by fields, and the electric and magnetic fields were unified into a single electromagnetic field by Maxwell in 1865.
For quite a while that seemed to be it. In 1915 Einstein's theory of general relativity and Maxwell's theory of electromagnetism were completely compatible, and in that sense were unified in the classical sense. Even the shocking advent of quantum mechanics ten years later did not change the inventory of force fields.
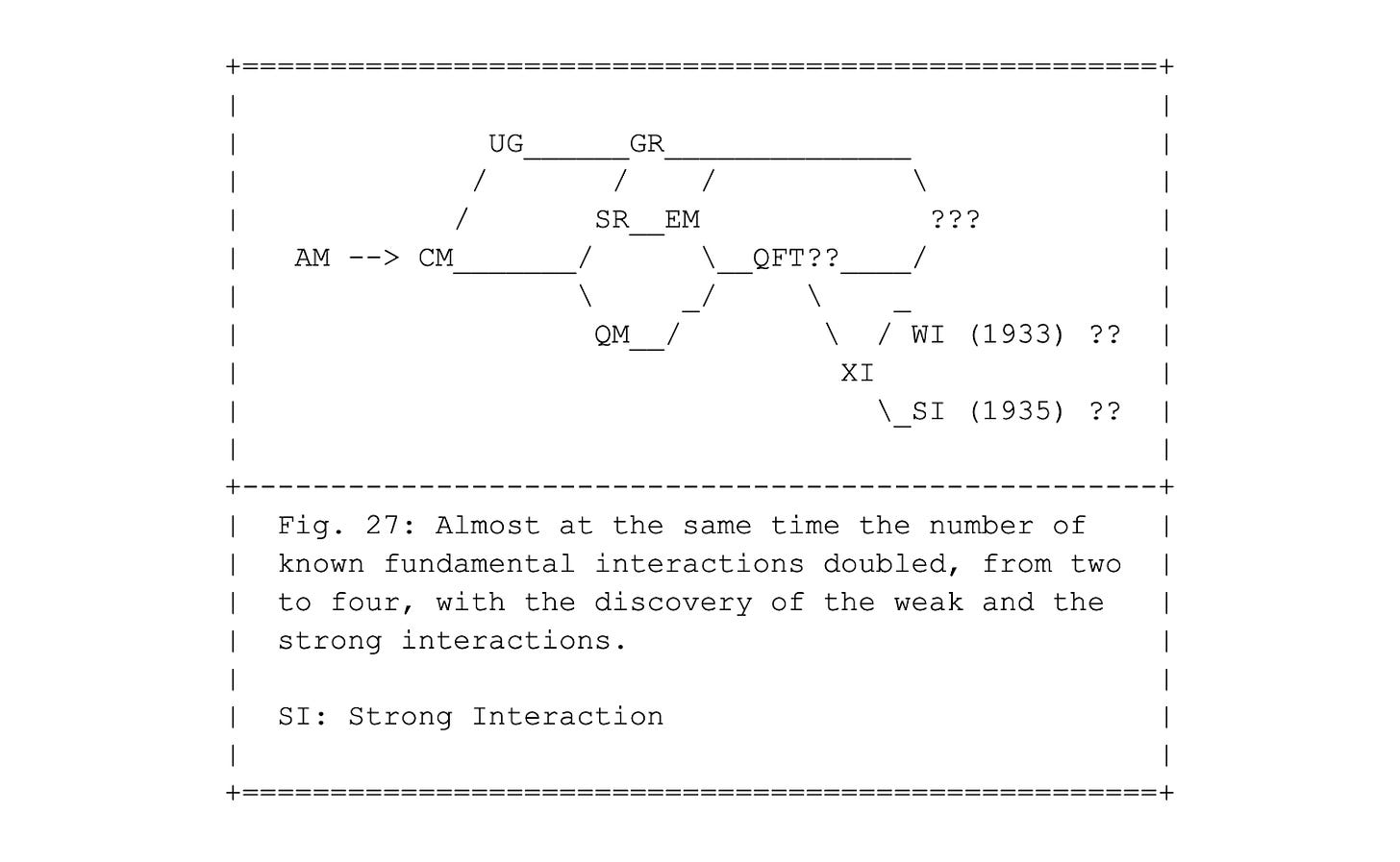
However, in 1933 a completely unexpected new "interaction" was discovered. Not sure about its character, as a force or a field or something else, and because it seemed intrinsically quite weak, it was called the "weak interaction", WI, as shown in Fig. 26.
In addition, only two years later, yet another one was discovered, stronger than the weak interaction, and dubbed "the strong nuclear interaction", or "strong interaction" for short, SI, as shown in Fig. 27.
Unlike gravity and electromagnetism, the weak and the strong interactions have an extremely short range. They play important roles at a distance comparable to the size of a proton or neutron. Beyond that, their strengths decrease exponentially as a function of distance. In contrast, electromagnetism and gravity grow weaker as the inverse square of the distance. As a result, we can draw sparks from the hairs of a cat and we can play with magnets, but we need rather advanced specialized equipment to detect and study effects of the weak and strong interactions.
It would take forty years before the nature of the weak and the strong interactions was understood on a fundamental level. Rather than following the twists and turns of various theories and speculations, we will come back to these interactions in our next entry, #012, to see their surprisingly beautiful unification with electromagnetism.
QED: the first successful renormalization of a QFT
The next major milestone, after the formulation of the first theories of quantum mechanics in 1925, was the renormalization of at least one quantum field theory, QFT. The bottom line of what is called "renormalization" is the invention of mathematical techniques to avoid spurious singularities, or infinities, that prevent us from making specific predictions from the first generation of quantum field theories. Physicists had extracted some results from QFTs, starting with Dirac's equations in 1928, but until 1950 these attempts had been rather haphazard and not systematic in any way.
Things changed within a short period of a few years, centered on 1950. Quantum electrodynamics, QED for short, was established as the unification of quantum mechanics, special relativity and electromagnetism, into one consistent quantum field theory. Until then, it had not been clear to what degree QFT could give reliable predictions for the outcome of experiments. Soon, however, calculations in QED became some of the most accurate ones in all of physics. Currently, experiments and calculations agree to an accuracy of one in one hundred million.
As was the case for the discovery of quantum mechanics around 1925, where there were several main players involved, the situation was no different around 1950. The most flamboyant and original of them was Richard Feynman, one of the three who shared the Nobel Prize for the discovery of QED, while a fourth physicist, Freeman Dyson, was the one who showed how the theories of the other three could be translated into each other. Feynman gave a wonderful series of lectures on QED for a popular audience, 35 years later, which were published as "QED: The Strange Theory of Light and Matter."
Another look at history: the genealogy of QED
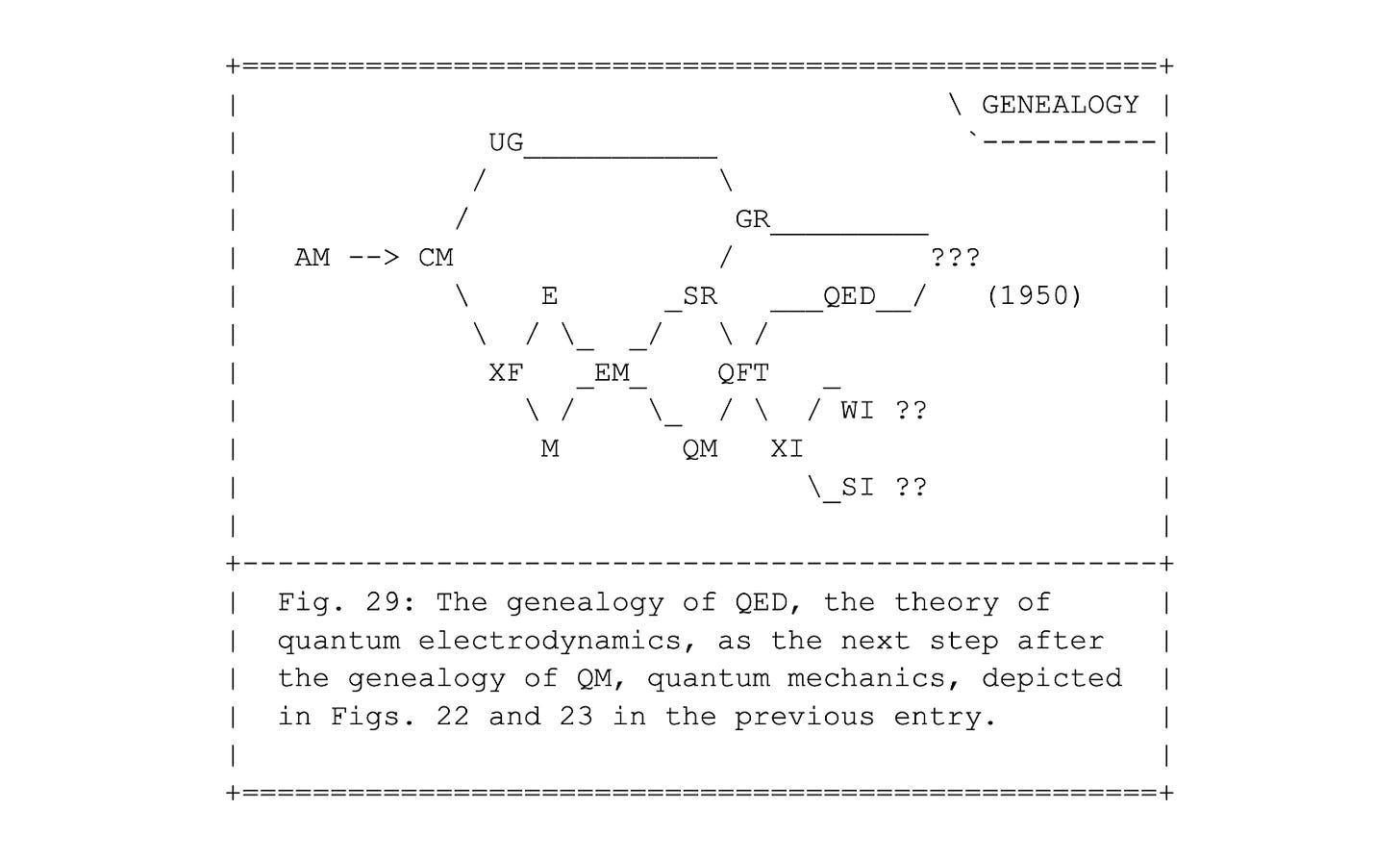
In the two previous entries, #009 and #010, I have sketched a pictorial genealogy of general relativity and of quantum mechanics, in Figs. 16 and 17, and in Figs. 22 and 23, respectively. In both entries I showed in each picture the historical order of discoveries leading to further discoveries, when reading from left to right. The equivalent genealogical diagram is given below in Fig. 29. As before, special relativity (SR) here *follows* electromagnetism (EM) in historical order, even though we now consider EM a relativistic theory *based* on SR, according to Fig. 28.
A quick preview of the next quarter century
In the first quarter century of quantum mechanics, it only took three years till the first quantum field theory, QFT, was introduced by Dirac. But from then on progress slowed down, and it would take more than two decades until QED, quantum electrodynamics, would become the first reliable QFT.
In our next entry, covering the second quarter since the discovery of quantum mechanics, we will see that the reverse would happen. For the first twenty years there was no real prospect that either the weak or the strong force could possibly be modeled as a QFT. More and more QED seemed like a unique success story, raising doubts as to wider applicability of QFTs in physics.
But then, in only a few years, from 1971 to 1975, just about everything fell into place, as we will see in the next log entry, our fifth and final entry of our picture book of progress in physics series.
A comparison of natural science and contemplation
We have seen in entry #002 how the science of matter could take off relatively quickly during the 17th century, given the millennia of written knowledge that provided necessary foundations for further progress. In our attempt to start a science of mind, the natural thing to do would be to similarly find inspiration in written knowledge, ideally with commentaries from individuals who are part of still living traditions based on that knowledge. The combination of both could then provide educated guesses for potentially useful working hypotheses -- stepping stones toward a scientific investigation of the human mind, using our mind as a laboratory, as we discussed in entry #004.
The big stumbling block in this rather obvious approach is that contemplative traditions with a written history do not resemble each other very much, at least at first sight. There are monotheistic contemplative traditions such as Judaism, Christianity and Islam, between which comparisons are relatively easier, given that they share the same roots. But comparing any of them with Taoism, say, will be a far greater challenge.
We saw at the beginning of this entry how matrix mechanics and wave mechanics seemed utterly different and incompatible at first. But within a year, they were shown to be not only compatible, but physicists had already started to develop a kind of dictionary to translate between those two theories. And using that approach, they demonstrated that the results for actual experiments were the same, where applicable.
It is my hope and expectation that similar developments will appear in a science of mind, once a community with a critical mass has grown around the idea of applying the scientific method to the area traditionally known as contemplation, as I have started to outline in a few preliminary contours in entry #003. We will pick up that thread again in far more detail in Parts 3 and 4 of our series of log entries, to begin with in entry #014. But for now, we can already point to an important hint that the first half century of quantum mechanics may offer us.
Another hint for a science of mind
At the start of our picture book of physics theories, in entry #008, I listed several hints toward the end that might become handy later on in our search for a science of mind. The main hint that we can glean from the current entry is that theories do not have to be internally consistent, let alone logically complete. As long as a new theory gives more accurate results than the previous best theory, by hook or by crook, the new theory is given pride of place. In that sense science is fully pragmatic and sometimes surprisingly opportunistic.
To wit: Dirac's theory was hailed as a breakthrough, because in some areas of application it was clearly successful, even though it failed in others. Two decades later QED was a major breakthrough because its predictions were far more accurate than any other theory in the first quarter century of quantum mechanics. Even so, it was still glaringly clear that at some higher energies its validity would break down. In short, in science you can't argue with success in applications, no matter how elegant or attractive less successful theories may seem to be.
Perhaps the main inspiration of all this for a science of mind is that very different views in contemplation, the equivalent of different theories in physics, may not be as incompatible as they may look at first sight. For contemplative traditions, the ultimate validity in terms of experiential depth of insight for a practitioner may not have an obvious relationship to the outer forms of the belief systems, used to introduce the practice.